下面是關(guān)于考研數(shù)學(xué)一、二、三中常微分方程部分的考試內(nèi)容與考試要求對比。

　　數(shù)學(xué)一常微分方程部分要求：

　　考試內(nèi)容

　　常微分方程的基本概念、變量可分離的微分方程、齊次微分方程、一階線性微分方程、伯努利(Bernoulli)方程、全微分方程、可用簡單的變量代換求解的某些微分方程、可降階的高階微分方程、線性微分方程解的性質(zhì)及解的結(jié)構(gòu)定理、二階常系數(shù)齊次線性微分方程　高于二階的某些常系數(shù)齊次線性微分方程、簡單的二階常系數(shù)非齊次線性微分方程、歐拉(Euler)方程、微分方程的簡單應(yīng)用;

　　考試要求

　　1、了解微分方程及其階、解、通解、初始條件和特解等概念;

　　2、掌握變量可分離的微分方程及一階線性微分方程的解法;

　　3、會解齊次微分方程、伯努利方程和全微分方程，會用簡單的變量代換解某些微分方程;

　　4、會用降階法解下列形式的微分方程：

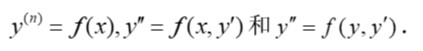
　　5、理解線性微分方程解的性質(zhì)及解的結(jié)構(gòu);

　　6、掌握二階常系數(shù)齊次線性微分方程的解法，并會解某些高于二階的常系數(shù)齊次線性微分方程;

　　7、會解自由項為多項式、指數(shù)函數(shù)、正弦函數(shù)、余弦函數(shù)以及它們的和與積的二階常系數(shù)非齊次線性微分方程;

　　8、會解歐拉方程;

　　9、會用微分方程解決一些簡單的應(yīng)用問題;

　　數(shù)學(xué)二常微分方程部分要求：

　　考試內(nèi)容

　　常微分方程的基本概念、變量可分離的微分方程、齊次微分方程、一階線性微分方程、可降階的高階微分方程、線性微分方程解的性質(zhì)及解的結(jié)構(gòu)定理、二階常系數(shù)齊次線性微分方程、高于二階的某些常系數(shù)齊次線性微分方程、簡單的二階常系數(shù)非齊次線性微分方程　微分方程的簡單應(yīng)用;

　　考試要求

　　1、了解微分方程及其階、解、通解、初始條件和特解等概念;

　　2、掌握變量可分離的微分方程及一階線性微分方程的解法，會解齊次微分方程;

　　3、會用降階法解下列形式的微分方程：

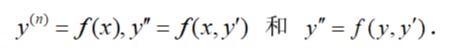
　　4、理解二階線性微分方程解的性質(zhì)及解的結(jié)構(gòu)定理;

　　5、掌握二階常系數(shù)齊次線性微分方程的解法，并會解某些高于二階的常系數(shù)齊次線性微分方程;

　　6、會解自由項為多項式、指數(shù)函數(shù)、正弦函數(shù)、余弦函數(shù)以及它們的和與積的二階常系數(shù)非齊次線性微分方程;

　　7、會用微分方程解決一些簡單的應(yīng)用問題;

　　數(shù)學(xué)三常微分方程與差分方程部分要求

　　考試內(nèi)容

　　常微分方程的基本概念、變量可分離的微分方程、齊次微分方程、一階線性微分方程、線性微分方程解的性質(zhì)及解的結(jié)構(gòu)定理、二階常系數(shù)齊次線性微分方程及簡單的非齊次線性微分方程、差分與差分方程的概念、差分方程的通解與特解、一階常系數(shù)線性差分方程、微分方程的簡單應(yīng)用;

　　考試要求

　　1、了解微分方程及其階、解、通解、初始條件和特解等概念。

　　2、掌握變量可分離的微分方程、齊次微分方程和一階線性微分方程的求解方法。

　　3、會解二階常系數(shù)齊次線性微分方程。

　　4、了解線性微分方程解的性質(zhì)及解的結(jié)構(gòu)定理，會解自由項為多項式、指數(shù)函數(shù)、正弦函數(shù)、余弦函數(shù)的二階常系數(shù)非齊次線性微分方程。

　　5、了解差分與差分方程及其通解與特解等概念。

　　6、了解一階常系數(shù)線性差分方程的求解方法。

　　7、會用微分方程求解簡單的經(jīng)濟應(yīng)用問題。

　　以上就是數(shù)一、二、三常微分方程部分的考考試內(nèi)容與考試要求，希望同學(xué)們繼續(xù)努力!